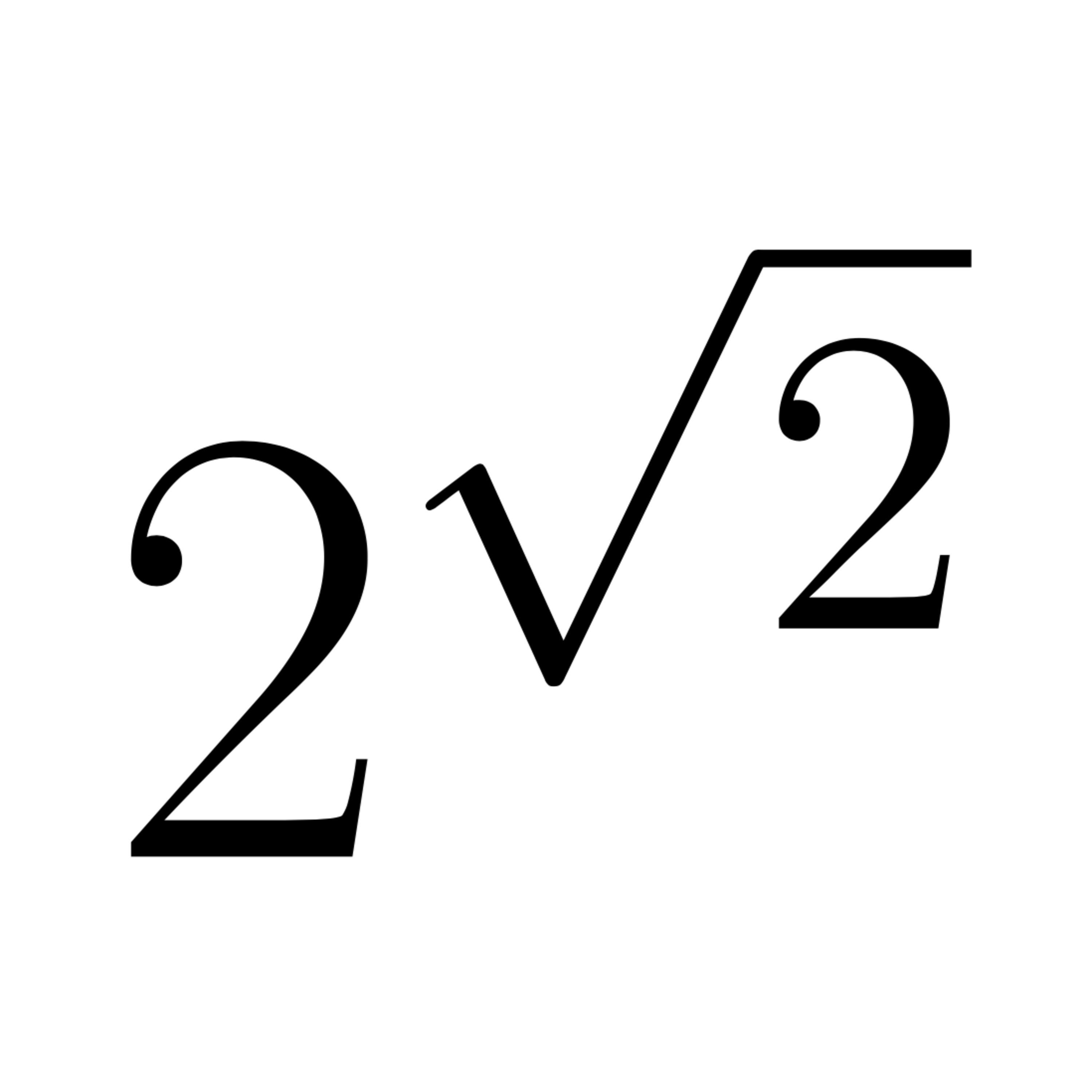Discover Well-defined & Wonderful
Well-defined & Wonderful

Well-defined & Wonderful
Author: profmoppi
Subscribed: 1Played: 9Subscribe
Share
© profmoppi
Description
In Well-defined & Wonderful we embarque on the quest to understand the core principles of mathematical analysis. Being based on a lecture course aimed at first year students in Germany the podcast highlights the most important aspects of the individual chapters of the course. The corresponding lecture notes will be available through marcus-waurick.de
37 Episodes
Reverse
The culmination point of the podcast well-defined & wonderful (for now, anyway) is the second part of the fundamental theorem. It combines the most important notions of the podcast so far: continuity, differentiation, and integration. We shall show that continuous functions on bounded and closed intervals always admit an anti-derivative. This anti-derivative is given as the integral of this function integrated with a variable right end point. The first and second part of the fundamental theorem lead to the substitution rule and the integration by parts formula. Finally we will also attempt to prove the second part of the fundamental theorem by providing the main tricks and glueing them together into one wonderful proof.
In this episode we are studying a first connection of differentiation and integration. More precisely, we will show that if a Riemann integrable function has an anti-derivative then the computation of the integral comes down to the evaluation of the anti-derivative. The proof provided uses a re-interpretation of the mean value theorem. A reorganisation of the terms involved in the statement of the mean value theorem leads to a relation of function evaluation and the integral of a step function with some height given by the derivative at some point of the function. A telescoping sum and a limit argument concludes the proof.
This episode is focussing on a different sort of monotonicity compared to the notions we have used before. Here, we view the integral as a mapping assigning numbers to (Riemann integrable) functions. Monotonicity of the integral then means that non-negative functions are mapped to non-negative numbers. Or, in other words, if one function is smaller than another; their respective integrals can be compared the same way. In related contexts such mappings on functions are also called positive. As an application, we provide a fundamental inequality for the integral — a continuous variant of the triangle inequality: The modulus of the integral of a function is bounded above by integral of the modulus of the said function.
This episode is concerned with providing another class of functions that are Riemann integrable. This class will be monotone functions and are neither contained nor are supersets of the step functions or continuous functions we have identified to be Riemann integrable already. The idea of proof for the desired result in the current episode is the construction of tailored step functions smaller and bigger than the monotone function so that the integral of the difference of the constructed functions gets smaller if the maximal distance of the partition points does so.
In this episode, we introduce the class of Riemann integrable functions. At the heart of the definition lies the wish to extend the intuitive notion for the integral of step functions on closed and bounded intervals to functions for which one can approximate the area between the function's graph and the x-axis by areas of rectangles. We then discuss that all continuous functions on a closed and bounded interval are Riemann in fact integrable - a fact that heavily relies on the property of uniform continuity.
The present episode asks a new question: How can one compute the area under the function graph of a real-valued function defined on an interval? It turns out that this question is not entirely trivial to answer. In order to have a first clear understanding of some pitfalls, we treat an elementary example case first: We discuss the notion of a step function. Then, the area under function graph — the Riemann integral — can be computed as a sum of certain rectangles. Before we embark to more challenging situations, we shall see that the so defined integral will be well-defined for step functions.
This episodes focusses on the mean value theorem and its consequences. One way of describing the mean value theorem is that the average velocity must be attained at some point. Reading this fact somehow backwards tells us some thing about the average velocity given some information about the derivative. Indeed, monotonicity can be obtained if the derivative has only one sign; also a sufficient criterion for the existence of extreme values can be shown. Other consequences like the generalised mean value theorem of the theorem of Bernoulli—l’Hospital are mentioned; for the precise statements we refer to the lecture noted however.
Picture from https://www.pngall.com/trekking-png/download/25141
Having defined the derivative of a function in the previous episode, we now turn to properties of the derivative and of the function in connection to the derivative. This episode is concerned with a first theorem asserting as much, namely Rolle’s theorem. This theorem tells us that the derivative of a differentiable function has a zero as long as it assumes one value twice. A consequence of this will be the mean value theorem, the consequences of which we address in the next episode.
Picture from https://www.flickr.com/photos/11703832@N08/16827652499
A more global viewpoint of the concept of differentiability is when a whole function is differentiable everywhere. In this case, we can define a mapping assigning each point to the limit of the difference quotient at this point. This map is called the derivative of a function. It is then of interest how operations on functions like multiplications, additions, quotients, compositions, etc behave under computing the derivative. It turns out that one can show certain rules of differentiation, which are also touched upon in this episode.
Picture from Nick Youngson CC BY-SA 3.0 Alpha Stock Images
This episode is concerned with the concept of Differentiability. Roughly speaking, we seek a quantitative method to assess the change (or rate of change) of a function. For this we consider its slope and try to define a slope at every single point in the domain of said function. Wherever this works, we call the function differentiable at this point. It turns out this notion is equivalent to the function being reasonably enough approximated by affine functions.
We will now take an even closer look into Euler’s formula this time. More precisely we will investigate whether there exists a real number such that the imaginary unit times this real number plugged into the complex exponential function will give the imaginary unit as a result. In fact, as it will turn out, this is equivalent to finding roots of the cosine function. Having identified the cosine function as a continuous function we the apply the intermediate value theorem to obtain existence of such a zero. The existence of such a zero alone is sufficient to obtain periodicity and symmetry properties for both sin and cos. The only zero of cos in the interval from 0 to 2 will be called pi/2, which gives a stand alone definition of the precise value of pi.
Picture taken from https://fsymbols.com/images/pi-pie.jpg
This episode is concerned with one of the most striking formulas in mathematics. Namely the relationship between sin, cos, and the complex exponential for purely imaginary arguments. To derive this formula, we require a closer look into the complex exponential function. The most important fact that we will derive is that no matter the modulus of the purely imaginary number put into the complex exponential the result will always be on the unit circle. Whether or not we reach all elements of the unit circle in the complex plane while running through all purely imaginary numbers remains to be seen in the next episode.
Picture taken from https://hyrodium.tumblr.com/post/106601751454/euler1
In this episode we introduce an extension of the exponential function to arguments from the field of complex numbers. We briefly address convergence of sequences and series of complex numbers. We recover several properties from the real exponential function also in the complex case. Most importantly, we also have the functional equation valid in the complex case; thus, this newly defined function is both never zero and continuous, much like the real exponential function.
This episode is concerned with the field of complex numbers. In fact, we shall motivate the emergence of `imaginary numbers’ — particularly their prototype representative i — via entirely nothing really imaginary. Representing numbers as such as geometric operations we shall see that the number i can be interpreted as an operation on the plane. Indeed, in order to solve the equation x times x equals negative 1 for x, we look at the -1 as point reflection through the origin, which is the same as rotation by 180 degrees. Hence, two rotations by 90 degrees yield the point reflection and, thus, a solution x for the equation in question.
Picture taken from https://www.flickr.com/photos/mythoto/3958500788
In this episode we demonstrate that the inverse of continuous functions (i.e., the inverse mapping - not to confuse with the point wise reciprocal) is, too, continuous. For this we show that once a continuous functions maps an interval one-to-one into the reals it is necessarily also strictly monotone (either increasing or decreasing). This observation eventually helps us with the proof of our desired result.
In this episode we provide the missing uniqueness part for our construction of general powers. More precisely, we will show that given any continuous function that satisfies the power law is actually a power. The technique to obtain this is by successively checking cases of increasing complexity: if the function satisfies the power law it behaves like a power for natural numbers, for integers, for rationals (using the uniqueness of the n-th root of non-negative numbers), and, finally, using continuity and density, for reals.
This episode is devoted to discuss a definition for what it means to raise a strictly positive real number to a real number. Up until now we were only able to do that for the exponential function, that is, we were able to raise e to any real number. In other words, the current episode deals with the method to change the basis for a power. The definition provided for instance serves as a means to define 2 raised to square root of 2, the provided expression is continuous in the exponent and makes use of the (natural) logarithm - the inverse function of the exponential function introduced in the previous episode.
In this episode we argue how and why we can devise an inverse function to the exponential function. Hence, we shall construct the logarithm and give precise reason why the logarithm exists and is indeed well-defined for any strictly positive real number. The existence part roots on the intermediate value theorem, the uniqueness part on the properties of the exponential function. The logarithm being the inverse of the exponential function is one of those functions that rather give the answer to a question (``To which power do I have to raise e to get a given number y?'') instead of being explicitly computable like the square or the reciprocal.
In this episode we introduce a new concept regarding continuity, namely uniform continuity. For continuity, for given deviation of function values, the allowed deviation of corresponding pre-images depends on the point, where continuity is analysed. In contrast, for uniform continuity, the allowed deviation of pre-images can be chosen independently of the point considered and only depends on the initially allowed deviation of function values. There are examples that show that uniform continuity is strictly stronger than continuity. However, if a function is defined on a sequentially compact metric space, continuity is already enough to yield uniform continuity.
This episode is concerned with another invariance property continuous functions have. After having introduced and exemplified sequential compactness, we provide some intuition behind it. Then we prove that images of sequentially compact spaces under continuous maps are themselves sequentially compact. The immediate application to the particular case of functions mapping into the real numbers shows that continuous real-valued functions defined on sequentially compact spaces admit their supremum and infimum; that is, the maximum and the minimum of the image exists.
Picture: William Murphy from Dublin, Ireland, CC BY-SA 2.0, via Wikimedia Commons