Audio note: this article contains 169 uses of latex notation, so the narration may be difficult to follow. There's a link to the original text in the episode description.

Abstract:[1]

Tarski's Undefinability Theorem showed (under some plausible assumptions) that no language can contain its own notion of truth. This deeply counterintuitive result launched several generations of research attempting to get around the theorem, by carefully discarding some of Tarski's assumptions.

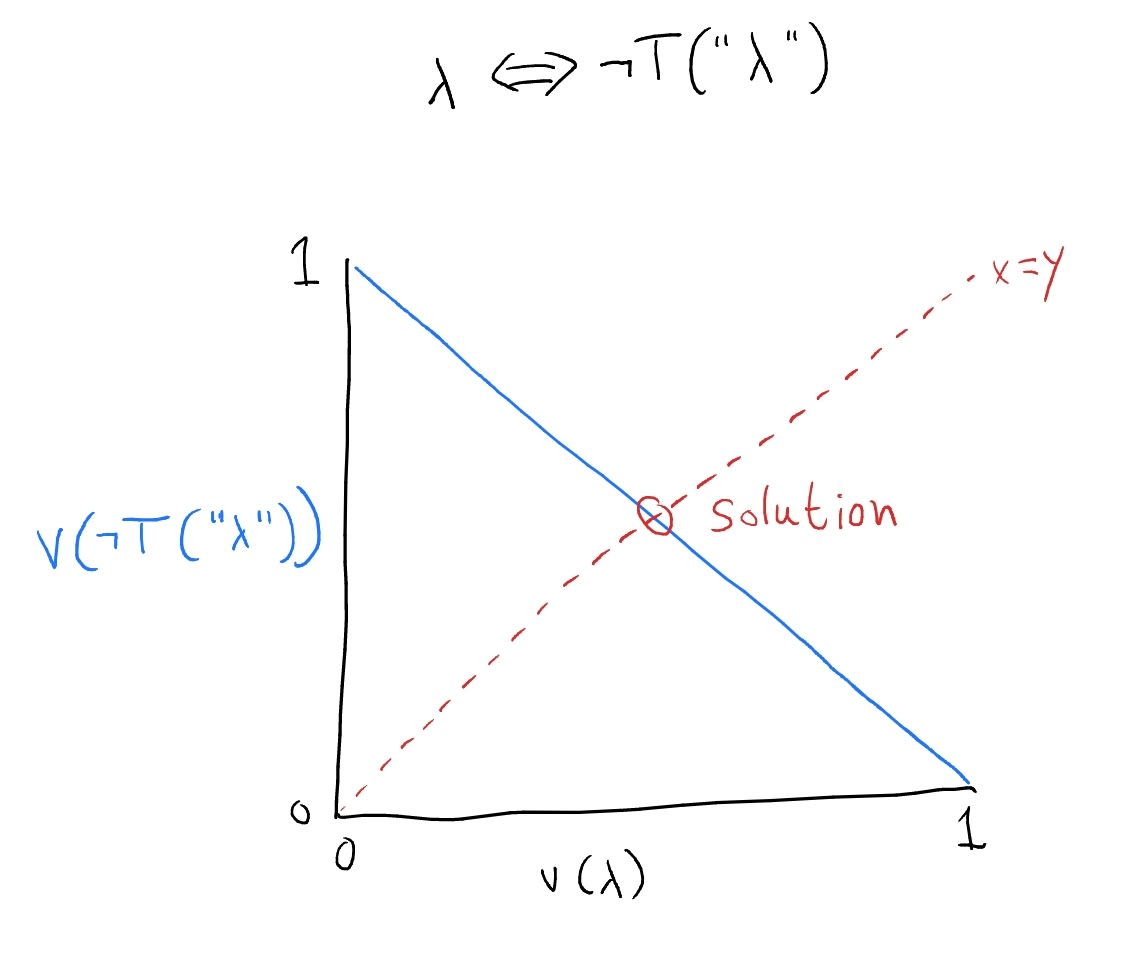
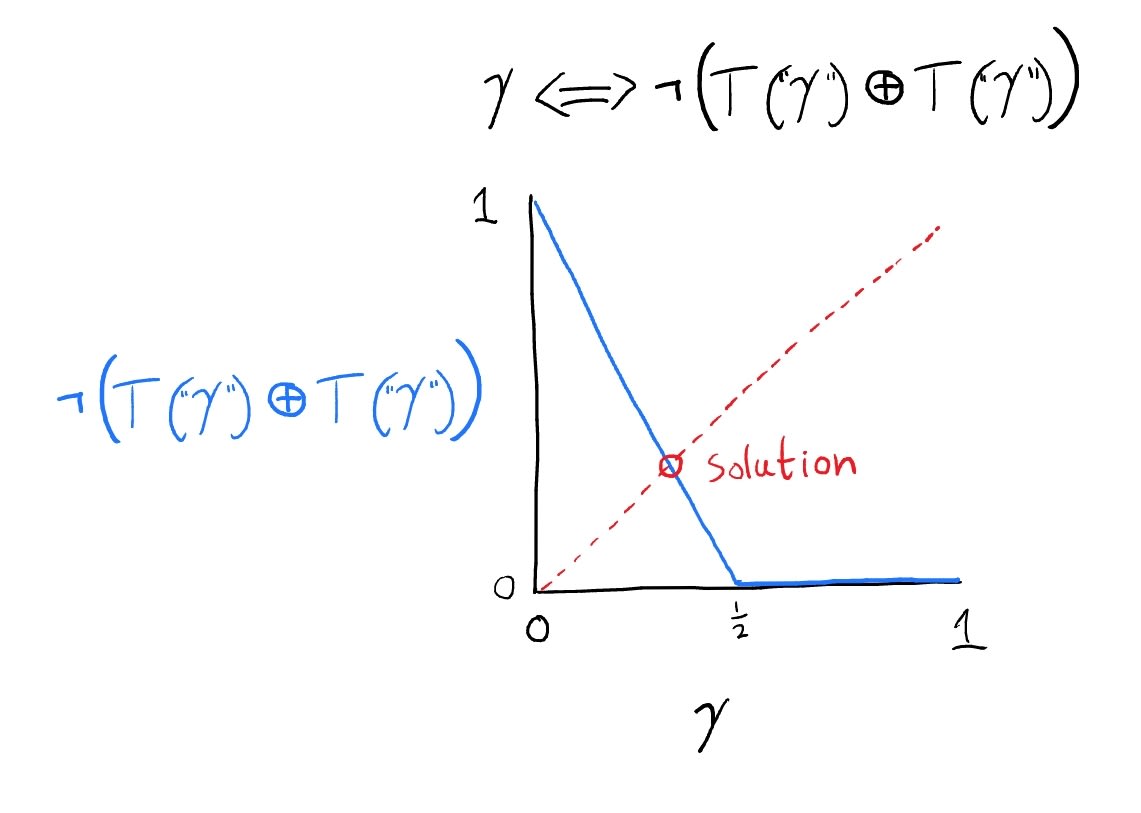
In Hartry Field's Saving Truth from Paradox, he considers and discards a theory of truth based on Łukasiewicz logic, calling it the "most successful theory so far" (out of very very many considered by that point in the book) and enumerating its many virtues. The theory is discarded due to a negative result due to Greg Restall, which shows that a version of the theory with quantifiers must be _omega_-inconsistent.

We consider this abandonment too hasty. The success of Łukasiewicz logic lies in postulating "between values" of truth, starting at _1 over 2_-valued sentences positioned precisely between true and false, and ending in the whole continuum of real values _[0,1]_. Why stop there? We propose a variant of the theory based on nonstandard analysis, which avoids [...]

---

Outline:

(01:42 ) Tarskis Theorem

(05:40 ) Łukasiewicz Logic

(07:17 ) Continuum-Valued Łukasiewicz Logic

(11:24 ) Restalls Theorem

(14:33 ) But _Ł_{\\infty}_\-truth is very nice

(17:15 ) Infinitesimal Truth

(18:37 ) Nonstandard Analysis

(20:17 ) Hyperfinite Quantification

The original text contained 2 footnotes which were omitted from this narration.

---

First published:

November 21st, 2025

Source:

https://www.lesswrong.com/posts/j3Cv94eEZTDFiLREW/rescuing-truth-in-mathematics-from-the-liar-s-paradox-using

---

Narrated by TYPE III AUDIO.

---