“Matrices map between biproducts” by jessicata
Description
Audio note: this article contains 98 uses of latex notation, so the narration may be difficult to follow. There's a link to the original text in the episode description.
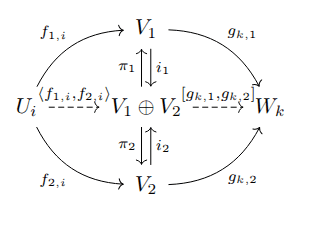
Why are linear functions between finite-dimensional vector spaces representable by matrices? And why does matrix multiplication compose the corresponding linear maps? There's geometric intuition for this, e.g. presented by 3Blue1Brown. I will alternatively present a category-theoretic analysis. The short version is that, in the category of vector spaces and linear maps, products are also coproducts (hence biproducts); and in categories with biproducts, maps between biproducts factor as (generalized) matrices. These generalized matrices align with traditional numeric matrices and matrix multiplication in the category of vector spaces. The category-theoretic lens reveals matrices as an elegant abstraction, contra The New Yorker.
I'll use a standard notion of a vector space over the field _mathbb{R}_. A vector space has addition, zero, and scalar multiplication defined, which have the standard commutativity/associativity/distributivity properties. The category _mathsf{Vect}_ has as objects vector spaces (over the field _mathbb{R}_), and as morphisms linear maps. A linear map _f : U rightarrow V_ between vector spaces U, V satisfies _f(u_1 + u_2) = f(u_1) + f(u_2)_ and _f(au) [...]
---
First published:
November 15th, 2025
Source:
https://www.lesswrong.com/posts/7wstHFRn3bHzSN2z3/matrices-map-between-biproducts
---
Narrated by TYPE III AUDIO.
---
Images from the article:
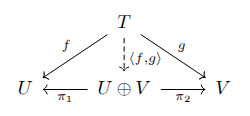
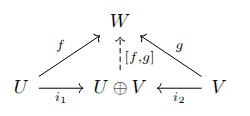
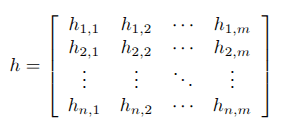
Apple Podcasts and Spotify do not show images in the episode description. Try Pocket Casts, or another podcast app.





