For our 61st episode, we bring back the presenter who appeared in our very first podcast episode, writer and translator Karen Margolis. Drawing from her own history in higher mathematics, Karen ably tells the tale of Germany’s Emmy Noether, who developed key theorems in theoretical physics and made important contributions to abstract algebra. Excluded from academic positions in Germany as a woman, she worked unpaid and under other lecturers’ names. Once she was finally allowed to teach in 1919, she had only 14 years until the Nazis banned her from universities, as a Jew. In American exile, she taught at the women’s college Bryn Mawr and occasionally at Princeton, though she felt she was not welcome at “the men’s university, where nothing female is admitted.”  Nowadays, everything from fellowships to a crater on the moon has honored Emmy, so it was clearly our turn to do so. 

DLS co-founder Katy Derbyshire joins producer/host Susan Stone to introduce things. 

<figure class="wp-block-audio"></figure>

Also available on Spotify, Apple Podcasts, RadioPublic, Pocket Casts, Stitcher, Google Podcasts, and Acast. You can download the transcript, created by Susan, here.

Show notes:

<figure class="wp-block-image size-large is-resized"><figcaption class="wp-element-caption">Emmy Noether with her three brothers</figcaption></figure>



<figure class="wp-block-image size-large"><figcaption class="wp-element-caption">The plaque on the building where Emmy Noether was born, in Erlangen</figcaption></figure>



<figure class="wp-block-image size-large"><figcaption class="wp-element-caption">An early supporter, the British mathematician David Hilbert with his trademark hat</figcaption></figure>



<figure class="wp-block-image size-large"><figcaption class="wp-element-caption">Title page of Emmy Noether’s doctorate, which translates as “On Complete Systems of Invariants for Ternary Biquadratic Forms”</figcaption></figure>



<figure class="wp-block-image size-large">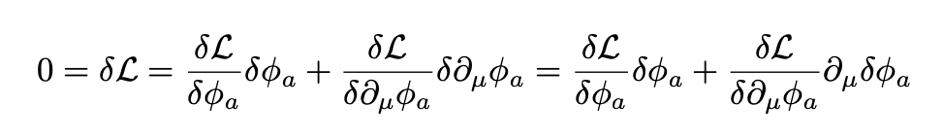<figcaption class="wp-element-caption">And a typical example of one of her innovative and exciting algebraic formulae</figcaption></figure>



<figure class="wp-block-image size-large"><img loading="lazy" width="749" height="1023" data-attachment-id="4276" data-permalink="https://deadladiesshow.com/en7/" data-orig-file="https://deadladiesshow.files.wordpress.com/2023/03/en7.png" data-orig-size="943,1289" data-comments-opened="0" data-image-meta="{"aperture":"0","credit":"","camera":"","caption":"","created_timestamp":"0","copyright":"","focal_length":"0","iso":"