Audio note: this article contains 86 uses of latex notation, so the narration may be difficult to follow. There's a link to the original text in the episode description.

Here's a conceptual problem David and I have been lightly tossing around the past couple days.

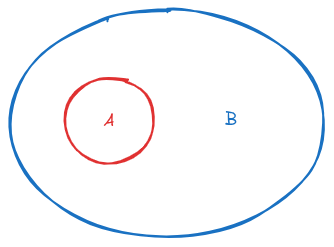
“A is a subset of B” we might visualize like this:

 

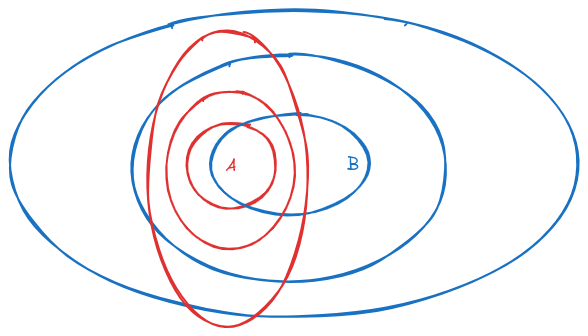
If we want a fuzzy/probabilistic version of the same diagram, we might draw something like this:

 

And we can easily come up with some ad-hoc operationalization of that “fuzzy subset” visual. But we’d like a principled operationalization.

Here's one that I kinda like, based on maxent machinery.

Background Concept 1: _E[-logP[X]] leq H_P(X)_ Encodes The Same Information About _X_ As _P_ Itself

First, a background concept. Consider this maxent problem:

_text{max}_{P’} -sum_X P’[X] logP’[X] text{ s.t. } -sum_X P’[X] logP[X] leq -sum_X P[X] logP[X]_

Or, more compactly

_text{maxent}[X] text{ s.t. } E[-logP[X]] leq H_P(X)_

In English: what is the maximum entropy distribution _P’_ for which (the average number of bits used to encode a sample from _P’_ using a code optimized for distribution _P_) is at most (the average number of bits used to encode a sample from _P_ using a code optimized for _P_)?

The solution [...]

---

Outline:

(01:10 ) Background Concept 1: _E\[-logP\[X\]\] \\leq H_P(X)_ Encodes The Same Information About _X_ As _P_ Itself

(02:35 ) Background Concept 2: ... So Let's Use Maxent To Fuse Distributions?

(05:48 ) Something Like A Subset Relation?

---

First published:

November 18th, 2025

Source:

https://www.lesswrong.com/posts/wBpguFgkygpQEGSyX/an-analogue-of-set-relationships-for-distribution

---

Narrated by TYPE III AUDIO.

---